Dobros sucessivos – base 2.

Frequentemente medito nos números e sobre os números, faz parte da minha profissão. Muito cedo revelei alguma apetência pelos números em desfavor das letras. Uma evidência em sala de aula merecedora de registo foi o exemplo que dei à minha professora primária sobre os sucessivos dobros quando, o que se pretendia era o conhecimento da tabuada do 2. O dobro de 1 é o 2 e o dobro de 2 é 4 e a seguir vem o 8, 16, 32... A professora mandou-me calar quando passava pelo 1024. Hoje sabe-se, incompreensivelmente para alguns, que este valor corresponde a um kilobyte, uma vez que se trata de uma grandeza associada a um sistema de base 2 e, portanto, é a potência de base dois a que se pode atribuir o prefixo kilo, por ser a mais próxima de 1000 bytes.

Mas não querendo fugir à questão dos sucessivos dobros importa referir que essa sucessão pode ser vista como sendo 2⁰, 2¹, 2², 2³, 2⁴, … É importante que se reconheça que o antecessor de qualquer termo é sempre metade desse termo. Faço esta referência porque há uma tendência natural para dizer que o dobro de 2¹⁰ é 2²⁰. Cuidado!...

Só muito mais tarde descobri que o fascínio que tinha por estes números também era um padrão de referência para outras culturas. Os egípcios, por exemplo, não se preocupavam em saber a tabuada como nós a propomos aos nossos alunos. O mais importante para eles era saber duplicar uma vez que qualquer número, se não fosse uma potência de base dois, poderia ser obtido pela soma de potências de base dois.

Também a informática optou por desenvolver a sua linguagem num processo simples, onde apenas dois símbolos seriam o suficiente para representar qualquer valor. Tomando um “zero” como sendo um circuito interrompido e um “um” como estando ligado, todos os arranjos entre “zeros” e “uns” fariam da opção binária a escolha ideal para o desenvolvimento daquilo que hoje é o mais complicado para todos nós - o computador.

De acordo com a tabela seguinte é fácil reconhecer que qualquer número pode ser representado apenas com “zeros” e “uns” necessitando apenas das potências de base dois para a sua formação:

Para ajudar na análise da tabela podemos verificar, por exemplo, que o número 10 é representado por '1010' significando no sistema binário, 1x2³+0x2²+1x2¹+0x2⁰=10, ou seja 8+0+2+0.

Aproveitando a regularidade que se evidência na tabela, sugere-se a formação de listas de ordem 0, 1, 2, 3… tendo cada lista o nome do número do expoente da referida ordem. Começando pela lista de ordem zero (2⁰) devem ser incluídos todos os números que têm um “um” na coluna dessa ordem:

Para construir a lista de ordem 1, segue-se o mesmo critério. Apenas se incluem os números cuja representação binária, precisa de um “um”, nessa ordem.

O mesmo critério se deve aplicar para formar as restantes listas:

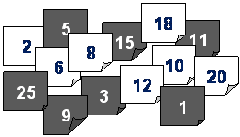
Uma vez organizadas 4 listas, verifica-se que são necessários 15 números para a formação das listas com o mesmo número de elementos. Note-se que todas elas acabam nesse número (2⁴-1). O número seguinte (2⁴), por se tratar de uma potência de base dois vai encabeçar a próxima lista (lista de ordem 4). Mas, considerando apenas estas quatro listas (0, 1, 2 e 3), pode-se pedir que pense num número até 15 e que revele as listas onde aparece. De imediato se fica a saber o número em que pensou. Quer dizer como? E se fizesse 6 listas, os números envolvidos seriam até qual?

Experimente descarregar aqui o ficheiro que lhe propõe 8 listas de números. Só tem de identificar as listas onde se encontra o seu número secreto. O computador encarrega-se de descobrir esse número.

Nota: depois de abrir o ficheiro Excel (office 2007), é necessário clicar em “opções” e optar por “activar este conteúdo” - macros.

Áreas e perímetros com abelhas (resp.)

Em relação ao artigo publicado neste blogue com o título Áreas e perímetros com abelhas a 1 de Agosto de 2008, proponho a seguinte análise:

Seguindo o conceito de uma pavimentação regular, o plano é pavimentado apenas com um tipo de ladrilho, cuja forma é um polígono regular. O polígono regular implica ter todos os lados de comprimento igual e ângulos internos com a mesma amplitude. Apenas o triângulo equilátero, o quadrado e o hexágono regular têm ângulos internos cujas amplitudes são submúltiplas de 360⁰. Quer isto dizer, que são os únicos polígonos regulares que pavimentam.

Facilmente se reconhece que o trabalho desenvolvido por uma comunidade composta por centenas de elementos é mais fácil se todos eles forem formatados para fazer o mesmo. Desta forma, não há a necessidade de discutir alterações ou a criação de novos projectos. Neste caso, o projecto das abelhas é dividir o plano em regiões idênticas, de forma que todas elas estejam sempre envolvidas no mesmo projecto. Assim, é compreensível que se adopte apenas um ladrilho para que seja feita a pavimentação (monoédrica).

Por outro lado, o rendimento do trabalho aumentará se para a conclusão do mesmo projecto recorrer à menor energia possível. É dentro desta lógica que importa saber qual a forma a adoptar para obter a maior área tendo o mesmo perímetro. Através do conhecimento matemático prova-se que o círculo é a forma geométrica ideal, tendo em vista a obtenção da maior área com o menor perímetro. De facto, entre as três figuras enumeradas anteriormente, o hexágono é aquela que se aproxima mais do círculo. Vamos lá perceber como é que as abelhas descobriram isso…

Fazendo o teste que é sugerido para uma mesma área:

Optando por triângulos equiláteros:

-- 135 palitos

-- ±9,5 palitos para acabar de fechar o rectângulo.

Total de 144,5 palitos

Optando por quadrados:

-- 76 palitos

-- ± 8,5 palitos para acabar de fechar o rectângulo.

Total de 84,5 palitos

Optando por hexágonos regulares:

-- 45 palitos

-- ± 19,5 palitos para acabar de fechar o rectângulo.

Total de 64,5 palitos

Comprova-se que para um menor consumo energético na construção dos favos, as abelhas estão certas em optarem pelos hexágonos.

Resto, excesso ou diferença

Quando mentalmente não se consegue efectuar a operação matemática desejada é nessa altura que se costuma recorrer ao algoritmo conhecido. Seguir um processo institucionalizado dá confiança a quem o pratica embora, por vezes, o praticante do algoritmo não atribua significado ao processo utilizado. Mas a aprendizagem matemática deve visar sempre a compreensão dos procedimentos e, por conseguinte, contribuir para se dar significado às rotinas.

Este objectivo não é um a meta fácil, principalmente nos primeiros anos de escolaridade onde é necessário o recurso a algoritmos para efectuar operações que ainda não foram conceptualizadas. A subtracção é o exemplo de uma operação que recorre a um algoritmo que, em caso pontuais, é de difícil compreensão. Refiro-me a situações em que é necessário recorrer a artifícios matemáticos para tornar possível esta operação, como seja nos casos de em que o algarismo do aditivo é inferior ao subtractivo.

A meu ver, a institucionalização do algoritmo só deve ocorrer quando o cálculo mental se revelar incapaz para se realizar a operação, ou quando outras técnicas utilizadas de forma compreensiva forem reconhecidas como sendo menos eficazes na obtenção de resultados mais rápidos. Mas o querer atingir objectivos muito rápidos no currículo do aluno faz com que a mecanização de procedimentos se antecipe à consolidação conceptual de respectiva operação.

No caso da subtracção, penso que seria importante analisar-se em primeiro lugar o significado da operação, pois pode tratar-se de um excesso, noutros casos de uma diferença ou ainda de um resto, dependendo do contexto onde se insere. Mas, à margem de situações concretas e abusando um pouco da abstracção matemática poder-se-á fazer uma breve análise a estes conceitos.

Por exemplo, 43 pode ser decomposto na adição 40 + 3 podendo, o 3, ser visto como sendo o resto que vai para além de 40. Portanto, perante a subtracção 43 – 40, poderemos entendê-la como querendo procurar o número que resta, para além do 40, para chegar ao 43.

Segundo este raciocínio e, tomando como outro exemplo a subtracção 54 – 26, pretendo determinar o que resta para além do 26 até ao 54. Assim, poderei decompor o 54 numa soma de duas parcelas de modo a obter 26. Este processo poderá ser feito de forma gradual de acordo com as capacidades de cálculo mental de cada utilizador, transferindo valores de uma parcela para a outra, criando adições equivalentes:

Uma outra interpretação seria por exemplo entender 54 – 26 como procurar a diferença que vai de 26 para 54. Neste caso, posso partir do 54 e ir retirando valor até atingir o 26. Depois basta adicionar os valores retirados;

Por outro lado, 54 – 26 pode ser interpretado como sendo o excesso que vai além de 26 até 54. Neste caso poderia seguir outro procedimento que consta no apuramento do valor em excesso. A sua representação poderia ser a seguinte:

Estes são três exemplos de sugestões algorítmicas que podem ajudar a superar a dificuldade na subtracção quando o algarismo do aditivo é inferior ao subtractivo. Para além destas sugestões algorítmicas da subtracção, deixo a representação de uma outra que era muito usual antigamente. Por exemplo, a seguinte subtracção: 2546 - 1794.

Embora se trate de um algoritmo moroso, que vantagem lhe pode ser reconhecida em relação ao nosso algoritmo tradicional?

O papel que usamos… (resp.)

Ao artigo publicado neste blogue com o título “O papel que usamos…” a 30 de Julho de 2008, proponho as seguintes respostas aos desafios lançados.

Seguindo a regularidade da tabela obtém-se as dimensões das folhas A₈, A₉ e A₁₀.

1. 2¹⁰=1024; A folha A₀ dá origem a 1024 folhas A₁₀

2. São necessárias 1024 folhas.

3. Para uma resma de papel A₄ são necessárias 500/16=31,25 folhas A₀. Então o peso da resma é 31,25 x 80 = 2500g

4. Uma folha A₀ dá origem a 2⁷ folhas A₇. Assim, o prisma é formado por 5 x 2⁷= 640 folhas. Logo, cada folha tem de espessura 64mm/640=0,1mm. Recorrendo à folha de cálculo Excel é fácil verificar que 0,1mm x 2³³=429496,7mm o que corresponde aproximadamente a 429m, portanto basta fazer 33 dobras sucessivas.

Quadratura do rectângulo

Faz parte do currículo académico da escolaridade básica, conhecer e saber determinar os pontos notáveis de um triângulo. Não é difícil memorizar os procedimentos para determinar, por exemplo, o circuncentro tendo em vista a realização de uma prova de exame. No entanto, a aplicação desse conhecimento matemático na vida real, de um modo geral, escapa à maioria dos estudantes. Isto faz-nos reflectir, afinal para que aprendemos matemática se não sabemos aplicar o conhecimento? Talvez uma das razões dos índices de sucesso nesta disciplina serem tão baixos se deva ao facto da escola não conseguir tornar relevante a importância do estudo da matemática.

Repare-se no exemplo de três amigos que pretendem encontrar-se todos à mesma distância de suas casas. Afinal, mais importante do que determinar o circuncentro de um triângulo, que parece não servir para nada, seria resolver um problema concreto onde é necessário aplicar o mesmo conhecimento matemático. Se aqueles amigos tivessem a oportunidade de desenvolver o seu raciocínio geométrico, poderiam não se lembrar do nome, mas provavelmente o problema estaria resolvido.

Há muitas descobertas matemáticas que sendo uma paixão para os mais aficionados por esta ciência, para outros são entendidas como meras futilidades. Um exemplo será saber a relação que existe entre a altura de um triângulo rectângulo, tendo por base a hipotenusa, e os segmentos que a formam separados pelo pé da sua altura.

Isto é: se [AD]=h; [BD]=a e [DC]=b que relação existe entre h, a e b?

O recurso à trigonometria pode ser uma das formas de encontrar essa resposta:

· O triângulo é rectângulo, logo α e β são ângulos complementares: cosβ= senα assim como senβ=cosα

· a+b é a hipotenusa do triângulo

por outro lado,

Assim, se compreende a existência da proporcionalidade:

ou seja,

Da interpretação desta relação, pode fazer-se a seguinte leitura: se considerarmos a base de um triângulo rectângulo a sua hipotenusa, então a sua altura é a média geométrica dos segmentos formados pelo pé da altura e os extremos da hipotenusa.

Este conhecimento, sem interesse aparente, pode servir de base a novos conhecimentos e a novas descobertas matemáticas. É este o sentido deste artigo. Com base neste conhecimento e com um pouco de pensamento geométrico, como se poderá interpretar os seguintes procedimentos?

Reconhecendo maior valor matemático àquele que produz o problema do que aquele que o resolve, deixo o desafio para que o leitor proponha um problema cuja solução exija este conjunto de procedimentos.

Estátua (resp.)

Em relação ao artigo aqui publicado com o título Estátua a 22 de Julho de 2008, sugere-me a seguinte resposta:

Um ensino conduzido pela sistematização de conhecimentos com especial incidência na resolução de exercícios em detrimento da resolução de problemas, em nada subsidia o desenvolvimento de novos conceitos e que capacite o aluno na aplicação dos seus conhecimentos, quer em situações de contexto matemático ou até mesmo não matemático.

O exemplo deste desafio é uma evidência em como grande parte das pessoas não consegue responder, pelo menos numa primeira abordagem, acertadamente.

Depois de muitos anos se terem passado após a escolarização básica, é muito provável que se tenha presente a regra a aplicar quando se pretende converter uma medida de volume, associada às medidas de comprimento no submúltiplo ou no múltiplo imediato. Com certeza que todos ainda se lembram de ter que se deslocar a virgula três “casas” de cada vez sem que, no entanto, fosse importante a compreensão deste procedimento. Talvez seja esta a razão porque a resposta a este desafio crie tanto embaraço.

É certo que, quando se trata de reduzir ou ampliar um objecto as suas medidas alteram nas suas três dimensões. Neste caso específico, a redução na sua altura é 10 vezes menor, o que implica uma redução no seu volume de 10x10x10. Assim, a quantidade de cobre necessária para a construção desta réplica será de apenas um milésimo da massa da estátua original. Logo 225 000kg:1 000 = 225kg

“E vai um …”

É muito vulgar a utilização da expressão “e vai um” quando realizamos uma operação aritmética. No caso da adição é facilmente compreensível a utilização desta expressão matemática. Quando adicionamos os valores de uma determinada ordem temos que transportar para a ordem seguinte o número de dezenas acumuladas na ordem anterior. Este procedimento deve-se ao facto de cada ordem admitir apenas um dígito.

Quer isto dizer que se eventualmente a soma dos valores de uma determinada ordem for, por exemplo, dezasseis (dez mais seis), ficam seis nessa ordem e vai uma dezena para a ordem seguinte - o mesmo que dizer “e vai um”. Quando a adição é constituída por várias parcelas pode acontecer que haja a necessidade de “irem 2, 3” ou o número de dezenas que acumula o somatório daquela ordem.

No caso da subtracção já não é assim tão fácil a interpretação do misterioso “e vai um”. A diferença encontrada é sempre inferior a dez, no entanto, por vezes utiliza-se o artifício do “e vai um”. Este procedimento ocorre quando numa determinada ordem é necessário subtrair um valor maior àquele que existe no aditivo.

Por vezes, costuma-se justificar este procedimento, embora sem fundamento científico, como sendo o método do empréstimo. Pede-se emprestado ao vizinho de cima e dá-se novamente ao vizinho de baixo. Isto é, imaginando que se pretende efectuar a seguinte subtracção 53 – 37, diz-se: sete para treze (pede-se 10 ao vizinho do lado) são seis, e vai um; três mais um (entrega-se no vizinho de baixo) são quatro, quatro para cinco fica um. A diferença é 16.

A bem da verdade, esta justificação não justifica nada. O que acontece, de facto, na subtracção é a verificação da ocorrência da invariância do resto quando se adiciona o mesmo número inteiro quer ao aditivo quer ao subtractivo. Neste exemplo, 53 – 37 = 63 – 47, por conveniência, o 63 é visto como sendo 50 + 13 e o 47 como sendo 40 + 7. Assim temos:

Utilizando a linguagem simbólica é o mesmo que:

53-37=

= (53 + 10) - (37 + 10) =

= (50 + 13) - (40 + 7) =

= 50 + 13 – 40 - 7=

= (50 - 40) + (13 - 7) =

= 10 + 6

Neste caso a técnica matemática utilizada consta de uma compensação. Se adicionamos 10 ao aditivo, então teremos que adicionar 10 ao subtractivo para que a diferença se mantenha. Será correcto dizer-se que se trata do método da compensação em vez do empréstimo.

Embora, a meu ver, seja este o método mais complicado para efectuar a subtracção, no entanto é o mais usual. Mais fácil seria a aplicação do verdadeiro método do empréstimo que consiste em transferir, no aditivo, uma dezena para a ordem de nível imediatamente inferior. A sua representação algorítmica poderia ser assim entendida:

Neste caso, o raciocínio seria traduzido da seguinte forma: sete para treze, seis unidades, e três dezenas para quatro dezenas, uma dezena.

Mas, o que me leva a reflectir sobre este assunto é o facto de num momento de avaliação diagnóstica ter surgido um aluno com um raciocínio completamente inovador no que diz respeito à técnica utilizada para fazer uma subtracção. No entanto, não deixa de ser muito interessante.

Perante a mesma subtracção (53 – 37) o aluno pensou alto: “de três, pretendo tirar sete – não é possível. Mas como posso tirar uma dezena na ordem seguinte, tenho que adicionar três nas unidades.  Então, três mais três são seis,

“e vai um”. Um mais três, quatro. Quatro para cinco, um”.

Não é fácil aceitar este procedimento sem uma reflexão prévia. Por isso, solicitei outro algoritmo (463 – 178) para que o aluno aplicasse o mesmo raciocínio.

Explicou de forma inequívoca:

- Dois mais três são cinco, e vai um;

- Um mais sete são oito, então dois mais seis são oito, e vai um;

- Um mais um são dois, dois para quatro vão dois.

Tratando-se de uma técnica infalível, importa encontrar o fundamento científico que sustenta o raciocínio deste aluno. É o desafio que fica para o leitor.

Conversões… (resp.)

Em relação ao artigo publicado neste blogue com o título Conversões a 21 de Julho de 2008, proponho a seguinte resposta:

Um decímetro cúbico não é mais que um cubo com um decímetro de aresta. Assim, em cada aresta cabem, em fila, 10 cubos com um centímetro de aresta. Aliás como esclarece a própria figura, sendo necessário 10x10x10=1000 centímetros cúbicos para preencher o espaço equivalente ao decímetro cúbico. A décima parte desse espaço pode ser visto como sendo uma placa com 10x10=100 cubinhos (centímetros cúbicos)

Portanto, não é nada de novo neste desafio na medida em que o procedimento mais usual para converter decímetros cúbicos em centímetros cúbicos é colocar 3 zeros à direita do número, o que equivale a aumentá-lo 1000 vezes.

Quer isto dizer que se pretender aumentar 10 vezes a aresta de um cubo, vou obter um volume 1000 vezes maior.

Imagine-se, no entanto, que tenho um pequeno cubo de pedra mármore com a massa de 3kg. Se pretender obter um novo cubo com o triplo da aresta, a previsão da sua massa, pela maior parte das pessoas, fica longe de se aproximar de 729kg. Porque será?

Média geométrica

Diga o que entende por média geométrica de um determinado conjunto de valores. Esta poderia ser uma questão de uma prova de avaliação de conhecimentos que, no âmbito dos conteúdos estudados naquele período, seria previsível que fosse posto à prova no próximo momento de avaliação. É por isso que no meu tempo de estudante, uma das estratégias adoptadas na preparação para as provas de avaliação, era decorar as definições que tínhamos no caderno diário. Neste caso, bastava decorar que a média geométrica de um determinado conjunto de dados é a raiz de índice n do produto desses valores elevados, cada um deles, à respectiva frequência absoluta.

A resposta correcta servia de garantia, para o professor, como o aluno se tinha apropriado daquele conceito. No entanto, o aluno continuava convicto de que aquele conhecimento não teria qualquer utilidade prática no futuro. A evolução do ensino da matemática acaba por valorizar a reflexão que o aluno faz sobre o seu próprio conhecimento ao ponto de retirar das provas de exames perguntas deste tipo. Se o aluno não consegue aplicar o conhecimento em novas situações, então é porque não se apropriou verdadeiramente do conceito matemático, logo, a avaliação feita não é a mais eficaz.

Imagine-se que em vez de ser pedida aquela definição, fosse pedido para determinar o comprimento do lado de um terreno com a forma de um quadrado que tivesse a mesma área de um outro terreno de 20m por 45m. Pretende-se, portanto, determinar a média geométrica destes dois valores. É o mesmo que encontrar um valor que, ao quadrado, seja igual ao produto de 20 por 45. O próprio aluno pode construir este conceito: área do terreno rectangular é 900m² (20x45m²). Para se obter o lado de um quadrado com a mesma área basta determinar a raiz quadrada de 900. O procedimento efectuado traduz-se na seguinte expressão:

Não é mais que a aplicação da definição dada de média geométrica. Assim se chega à conclusão que 30 é a média geométrica de 20 e 45. A partir desta experiência matemática torna-se evidente a importância deste conceito matemático facilitando a sua compreensão e a automatização do algoritmo sem ter de recorrer à “gaveta” onde estava memorizada a definição. Também não se corre o risco da informação se perder no caso de a “gaveta” permanecer muito tempo fechada.

No caso do leitor querer avaliar o seu próprio conceito de média geométrica e a importância que lhe possa dar em outras situações do quotidiano, proponho o seguinte desafio: a partir da figura, crie uma situação problemática sem que utilize a expressão “média geométrica”, mas cuja resposta seja dada pela seguinte expressão:

 

Pitágoras??... (resp.)

Em relação ao artigo publicado neste blog com o título “Pitágoras??...” a 18 de Julho de 2008, proponho a seguinte resposta:

É interessante como a maior parte das pessoas, com algum conhecimento matemático, quando são confrontadas com este exercício pensam sempre em recorrer ao teorema de Pitágoras para o poder resolver.

O desafio propõe-nos determinar o comprimento da diagonal do rectângulo. Sabe-se que as diagonais do rectângulo são de comprimentos iguais. É fácil reconhecer que a outra diagonal, não visível no esquema, é o raio da circunferência.

Sendo dado o raio da circunferência (5), então o comprimento de a=5.

Um momento de "matemática recreativa"

Hoje em dia, é reconhecido mundialmente a necessidade de qualquer país fazer fortes investimentos no sentido de elevar os índices de literacia matemática dos seus povos. Com um pouco de atenção, damos conta que qualquer comunicação, directa ou indirectamente, recorre a conceitos ou ideias matemáticas, sobretudo quando a mensagem é de conteúdo persuasivo. Valores estatísticos, ou o próprio número em si, acaba por ser um recurso fundamental na comunicação. É por isso que a comunicação matemática é hoje vista como sendo uma capacidade fundamental no currículo escolar de qualquer aluno.

Mas a comunicação matemática envolve conceitos matemáticos que, na maioria das vezes, não têm o mesmo entendimento entre receptores e emissores. Um exemplo muito vulgar é o recurso ao conceito de média para tornar o discurso mais convincente. No entanto, em grande parte dos casos não é pertinente a sua referência isolada, na medida em que a sua leitura não implica necessariamente alguma conclusão. Imagine-se o caso de um responsável de uma determinada empresa que, no seu discurso, para provar que os seus trabalhadores até são os mais bem pagos da região, recorre ao termo “média”. Na verdade, se o conceito de média for interpretado de forma correcta por todo o receptor, o argumento não seria suficientemente convincente dado que os vencimentos dos senhores gestores e administradores iludem os resultados apresentados.

Considere-se um exemplo mais simples. Quando se faz referência ao triplo de qualquer coisa, será que todos retêm a mesma ideia matemática? Não tenho dúvidas que a maior parte das pessoas responderia que se trata dessa coisa, três vezes. Outros, com um pensamento matemático igualmente válido, poderão pensar que se trata dessa coisa e ainda mais o seu dobro. No entanto, há quem pense que se trata de situações diferentes pelo simples facto de aparecer o conceito de dobro e o de triplo para explicar o mesmo fenómeno. Importa, pois, seleccionar o raciocínio que nos parece mais pertinente e adequado à mensagem que pretendemos transmitir de forma convincente, mas também inteligível.

Não serve de exemplo o que acontece no vídeo que se segue. Trata-se do Primeiro-Ministro de um país, a sua Ministra da Educação e um dos seus Secretários de Estado que divulgam um considerável aumento no rendimento subsidiário das famílias. A forma empolgada de o querer dizer, a iliteracia matemática que os limita, ou talvez não saberem ao certo o que querem comunicar, transformam uma comunicação simples em algo meramente difuso, onde eles próprios não se entendem…

Proponho assim o desafio ao leitor, depois de visionar o vídeo, poder interpretar a comunicação para tomar a decisão; o aumento do rendimento anunciado é de 100%, 200%, 300% ou 400%?

Mais um metro de perímetro

Que significado poderá ter o ente matemático 2πr? É normal que qualquer aluno, a partir do 2º Ciclo do Ensino Básico, diga que se trata do perímetro de um círculo cujo raio é r. Será que nos podemos dar por satisfeitos quando o aluno aplica a fórmula para calcular o comprimento de uma circunferência?

Tenho vários exemplos de alunos que aplicam bem a fórmula para o cálculo do perímetro quando lhes é dado o raio ou até o diâmetro. No entanto, porque razão grande parte destes alunos ficam sem resposta e outros arriscam com grande erro, quando lhes é pedido para fazerem uma estimativa sobre o número de diâmetros que cabem no perímetro de um dado círculo?

Na verdade, nem todos os alunos atribuem o mesmo significado a “pi”, embora saibam que é um valor aproximado de 3. Importa, pois, que o professor interrogue: três, quê?

Será que aqueles que são mais desenvoltos no domínio desta noção, de relacionar o perímetro de um círculo com o seu diâmetro, estão à altura de interpretar, em toda a sua plenitude, estas relações?

Eu estava convencido que não necessitava de reflectir mais sobre esta relação, até ao dia em que, já no ensino superior, o meu ilustre professor, Domingos Rijo, colocou à turma o seguinte desafio:

Imaginem uma esfera do tamanho do nosso planeta e que passamos uma corda em toda a sua volta de modo a obtermos o perímetro do seu maior círculo. A essa corda acrescentamos um metro de corda. Seguramente, vamos obter uma folga como ilustra a figura. Será que essa folga é suficiente de modo a passar por ela um gato?

Foi unânime a intuição matemática da turma em admitir que seria insignificante o aumento de um metro em todo aquele comprimento de milhares de quilómetros de corda. Portanto, a folga criada seria insuficiente para que passasse um gato.

A mesma experiência foi proposta numa bola de futebol. Da mesma forma, acrescenta-se um metro à corda que corresponde ao perímetro do círculo máximo da bola. Nesta segunda experiência, ninguém hesitou em reconhecer que a folga criada com o aumento da corda já seria mais que suficiente para passar um gato.

Mas, de acordo com o conhecimento da relação entre o diâmetro do círculo e o seu perímetro, podemos afirmar que está na razão aproximada de 1 para 3. Quer isto dizer que para um diâmetro com uma unidade de comprimento, obtemos um perímetro aproximado de 3 unidades de comprimento. Assim, na razão inversa, um perímetro de um círculo com uma unidade de comprimento, corresponde a um diâmetro aproximado de uma terça parte. Então, nas experiências anteriores, como o aumento do perímetro era o mesmo, implica um aumento no diâmetro no mesmo valor, isto é, aproximadamente uma terça parte de um metro.

Imaginando que a experiência era feita com uma bola de golf e admitindo que uma folga de 10 cm é o suficiente para um gato passar, de quanto se teria de aumentar a corda para que o gato pudesse passar entre a bola e a corda? E em relação ao mundo, quanto teria de ser esse aumento?

A Escada dos Bombeiros (resp.)

Em relação ao artigo publicado neste blogue com o título A escada dos bombeiros a 17 de Julho de 2008, proponho a seguinte resposta:

A forma como o problema é colocado talvez alvitre uma resposta que nos pareça evidente e, por conseguinte, imediata. Neste caso, a maioria das pessoas, pensa adicionar 12 com metade do seu valor, obtendo assim: 12+6=18.

Assim sendo, o comprimento da escada seria de 18 metros, o que leva a concluir que metade desse comprimento seja 9 metros. No entanto, ao fazer a verificação do resultado obtido, de acordo com o enunciado, a escada tem 12 metros mais metade do seu comprimento total, ou seja, 12 + 9 = 21. O resultado surpreende na medida em que não se confirma o comprimento de 18 metros.

Esta é uma situação que exige, do ponto de vista matemático, o simples conceito de metade. É certo que a unidade, neste caso, a escada dos bombeiros tem duas metades (necessariamente iguais).

Se a escada tem 12 metros, mais metade, quer dizer que a outra metade são os 12 metros. Tratando-se de juntar duas metades só poderemos adicionar 12 com 12.

Deste modo, sabe-se que a escada não tem 18 nem 21, mas sim 24 metros.

Uma questão de percentagem…

Com a aproximação da época balnear, aumenta a preocupação dos agentes responsáveis pela saúde pública face ao apetite pelo “trabalho” excessivo, onde a maioria das pessoas se empenha na maior produção do seu “bronze”. Isto talvez se deva ao facto de este “trabalho” ser o único que contraria as leis da Física, uma vez que pode ser realizado sem qualquer movimento.

A desidratação é um dos problemas em questão, daí as recomendações surgirem em todos os meios de comunicação social para que ninguém seja apanhado desprevenido. Mesmo assim, há sempre casos a relatar devido à falta de controlo dos índices aquosos. Não é por acaso que este solvente, imprescindível ao bom funcionamento de qualquer organismo vivo, é o constituinte do nosso organismo em maior percentagem.

À medida que a idade do ser humano vai avançando a percentagem de água no seu corpo vai diminuindo, seguindo quase um processo de desidratação. A partir dos 60 anos de idade, a percentagem de água no seu corpo é praticamente responsável por metade do seu peso. No caso das crianças, nos seus primeiros anos de vida, a percentagem de água no seu corpo é muito elevada, chegando a valores próximos de 80%.

Pelo que digo, nem parece que hoje o assunto seja matemática. No entanto, para que seja possível a compreensão do texto é necessário ter presente um conceito matemático – a percentagem. Nos dias de hoje, a solicitação a esta noção é tão grande que todo o público, mesmo não tendo uma apropriação plena deste conceito, de uma ou outra forma, certamente já incluiu este termo no seu discurso. Quanto mais não seja para saber o valor do seu vencimento após o anúncio de um possível aumento.

É no sentido de poder aferir se o leitor tem um bom domínio deste conceito que proponho o desafio de hoje. Trata-se de uma adaptação de um problema proposto pelo prof. Nuno Crato de um recente livro seu intitulado “A Matemática das Coisas”, onde alvitra de forma muito curiosa, como uma melancia pode reduzir substancialmente o seu peso condicionado por uma suposta perda mínima de água.

Analise-se, então, o que poderia suceder com uma criança de 3 anos, onde supostamente a percentagem de água no seu corpo é de 80%. Fica claro que admitimos, neste caso, que a massa sólida do seu corpo corresponde a 20%.

Vamos imaginar que os pais da Maria, em férias na praia, estão tão empenhados no “trabalho do bronze” que se descuidam e deixam que a percentagem de água no corpo da sua filha passe a ser idêntica à do seu avô. Esta desidratação, na criança, fez com que a percentagem de água no seu corpo passasse a ser na ordem dos 60%. Será que se pode considerar um descuido grave por parte dos pais? Imaginando que a Maria pesava 14kg e que sua perda de peso se deve exclusivamente à perda de água, quanto pesa agora a criança?

Antes de fazer os seus cálculos, sugiro que faça em primeiro lugar uma estimativa de quanto passaria a ser o peso da Maria. Só depois deve confirmar a sua estimativa. Mas se o resultado indicar que a criança passa a ter um peso superior a 11kg é porque cometeu um erro de cálculo ou de interpretação. Se for o caso, tente de novo. Não desista até encontrar o resultado certo. Um valor plausível para a solução do problema é garantidamente inferior a 8Kg.

Génio matemático no cálculo mental

A competência matemática inclui também a capacidade de fazer boas estimativas o que, na maior parte das vezes, é necessário um bom cálculo mental. Mas para o desenvolvimento desta capacidade é fundamental ganhar o hábito de calcular mentalmente, embora seja difícil resistir aos recursos tecnológicos, cada vez mais acessíveis, e que nos facilitam estas tarefas mentais.

Não obstante, nem todos têm o mesmo entendimento sobre este conceito. Aplicar um algoritmo mentalmente poderá ser considerado cálculo mental? Isto é, trabalhar com algarismos é o mesmo que trabalhar com números? O desenvolvimento do cálculo mental necessita do conhecimento das propriedades das operações coadjuvado com muitas experiências matemáticas na procura de relações numéricas. No entanto, o desenvolvimento de estratégias facilitadoras do cálculo mental poderão dar origem a novas sistematizações e por conseguinte, o estabelecimento de algoritmos específicos que poderão estar ao serviço do cálculo sem que, no entanto, seja mental.

O vídeo do génio matemático dá-nos conta disso. Na primeira parte do vídeo é explicada uma estratégia muito interessante que pode facilitar a aprendizagem da tabuada de multiplicar de uma forma diferente. Todavia, é necessário saber a tabuada até ao "cinco." Esta curiosidade matemática também pode ser consultada num artigo aqui publicado ou, através do ppsx também aqui disponibilizado.

Na segunda parte do vídeo, o jovem matemático consegue impressionar a plateia ao fazer a divisão de um número por cinco a partir de um algoritmo que todos deveriam interpretar: multiplicar por 2 e dividir por 10 é o mesmo que dividir por 5. Trata-se de uma estratégia muito útil, na medida em que é mais fácil encontrar, mentalmente, duas décimas de um número do que a sua quinta parte.

Já na terceira parte do vídeo, a apresentadora deixa revelar a sua cumplicidade com o jovem, uma vez que propõe os números que podem fazer brilhar o desempenho do petiz. Esta terceira situação já não resulta com todos os números.

O produto da percentagem por um número que termina em dois zeros faz com que o problema se resuma ao produto entre dois números com dois algarismos. Importa agora saber que propriedades têm estes números ou que relação existe entre eles para que a estratégia adoptada no seu produto resulte em pleno.

Repare-se que a estratégia utilizada para a multiplicação destes dois números é a mesma que pode ser aplicada quando se pretende determinar o quadrado de um número de dois dígitos cujo algarismo das unidades é cinco.

Por exemplo, 75x75; multiplica-se o “sete” pelo seu consecutivo (7x8=56) e junta-se 25. Temos assim, 75 x 75 = 5625. Repare-se que 25 é o quadrado do número das unidades.

Então, fica o desafio que consiste em descobrir a característica comum aos produtos 23x27, 44x46, 65x65 de modo a se poder aplicar a seguinte regra para o seu cálculo:

(a) determinar o produto do algarismo da dezena pelo seu consecutivo e juntar à direita, o produto das unidades.

23 x 27 = 621

44 x 46 = 2024

65 x 65 = 4225

Resposta: Rodas dentadas

Em relação ao artigo publicado neste blog com o título Rodas dentadas a 16 de Julho de 2008, proponho a seguinte resposta:

Trata-se de uma experiência muito interessante que pode ser facilmente concretizada com duas moedas.

Ao fazer percorrer em toda a volta de uma moeda uma outra de igual perímetro verifica-se que ao fim de dar uma volta completa, esta segunda moeda, dá duas voltas em torno de si própria. É compreensível, na medida em que o comprimento do seu perímetro corresponde a uma volta, e o comprimento do perímetro da outra moeda corresponde a outra volta.

Yakov Perelman explica que, quando um objecto roda descrevendo uma circunferência, ele dá sempre mais uma volta que aquelas que poderemos contar directamente. É por isso que se estivéssemos fora do nosso sistema solar a contar o número de voltas que o globo terrestre dá em torno de si próprio, ao longo de um ano, iríamos contar 366 voltas e ¼ ao contrário das 365 voltas e ¼ que seriam esperadas.

É interessante reflectir então sobre o movimento da Lua em torno da terra. É sabido que a lua mostra sempre a mesma face à terra. Este fenómeno deve-se ao facto de ter movimento de rotação ou, pelo contrário, de não rodar em torno de si própria?

Para ajudar a reflexão deixo aqui um caminho para um artigo de Luiz Vaz do Carmo.

Se não é par, é impar

A descoberta de relações numéricas pode ser vista como uma metodologia que, para além do desenvolvimento da capacidade de abstracção também favorece o raciocínio algébrico. É neste sentido que, numa visão matemática de natureza recreativa, proponho o desafio que poderá ser, também, uma ideia a aproveitar para ser levada à sala de aula na exploração de relações entre números pares e ímpares.

Considere-se então, os seguintes quadrados de papel com números inscritos em duas cores diferentes:

São necessárias duas caixas com as mesmas duas cores. O recurso ao origami poderá ser uma ajuda preciosa para a sua construção.

É pedido a uma pessoa que escolha dois papéis de cores diferentes e que os coloque, sem que ninguém veja, nas caixas. O objectivo é descobrir se os papéis colocados nas caixas respeitam, ou não, a correspondência das cores. Para isso é necessário recolher alguma informação matemática:

É necessário saber a soma do dobro do número que foi colocado na caixa branca com o triplo do número que foi colocado na caixa negra. Se a informação for verdadeira é o suficiente para saber se os papéis colocados nas caixas estão, ou não, com as cores trocadas.

Por exemplo, imagine-se que o valor da expressão é 46. Fico a saber que os papéis foram colocados com as cores trocadas nas caixas. Porquê?

Neste caso, o 5 (papel negro), foi colocado na caixa branca, o seu dobro é 10. O papel branco com o número 12 foi colado na caixa negra, cujo triplo é 36. A soma destes números é 46 (10+36).

De que forma poderá ser explicado este procedimento para ter a certeza que os papéis colocados nas caixas estão ou não de acordo com as suas cores?

Da capicua ao nove

O que é que “luz azul” tem de comum com “o bolo do lobo” ou com “o galo no lago” ou com “o namoro do romano”? Repare-se que “somávamos” goza da mesma característica.

Quando um conjunto de letras, números ou quaisquer outros símbolos colocados por uma ordem determinada podem ser lidos num ou noutro sentido, diz-se que estamos perante um palíndromo.

Quando esta curiosidade ocorre com os números, também damos o nome de capicua. Eu estive 27 anos à espera para comemorar um ano capicua. Entretanto, já comemorei outro. Mas o meu sobrinho Diogo vai fazer cinco anos e, muito provavelmente, não vai conseguir comemorar algum ano capicua. Porque será?

Já dei dados suficientes para se saber a minha idade. No entanto, o que eu pretendo é dar um pouco de atenção aos anos capicuas com 4 algarismos. O último é o ano formado apenas por noves: 9999. Qualquer ano capicua, se for separado ao meio, dá origem a dois números, em que um é o outro invertido. Considerando, por exemplo, o ano 3443, invertendo o 34 obtém-se o 43. A diferença entre estes dois números é 9.

Considerando, por exemplo, o ano 4774 e aplicando o mesmo procedimento obtém-se o número 27 (74-47=27). Mas também o 27 tem algo que se relaciona com o 9 (2+7=9). Repare-se ainda que a diferença entre 7 e 4 é 3 que, aparentemente, nada tem a ver com o 9, não fosse o 27 dividido por 3 dar 9. Não estarei eu a ser perseguido pelo 9? Será que isto é sempre assim?

Não falta a vontade para experimentar com outra capicua, por exemplo, 8338. Separado ao meio e fazendo a diferença: 83-38=45. Da mesma forma, 4+5=9. O mais interessante é que a diferença entre 8 e 3 é 5, e se aproveitarmos o 5 para dividir o 45 obtemos novamente 9.

Não tenho dúvidas em eleger o número nove como sendo o número de minha preferência! Caso o leitor não esteja convencido experimente fazer a seguinte experiência:

1. Escreva o número que representa a data do seu nascimento (ddmmaaaa).
2. Escreva novamente a data, mas noutro formato (aaaammdd).
3. Encontre a diferença entre esses dois números. Um exemplo poderia ser 19711205-05121971=14589234.
4. Adicione os algarismos do número obtido (ex.: 1+4+5+8+9+2+3+4)
5. Proceda da mesma forma em relação ao novo número obtido, as vezes necessárias até obter apenas um algarismo e delicie-se com o resultado.

Sem dúvida que este número tem características fantásticas. Esta paixão pelo número 9 deve-se ao facto de ter um papel muito especial no sistema de numeração decimal. Imagine que o nosso sistema de numeração não se organizava em grupos de dez, mas sim em grupos de cinco. Neste caso, qual seria o número que nos poderia surpreender com estas potencialidades?

Divisão chinesa (?) com números decimais

Ultimamente tenho utilizado e praticado várias divisões com o algoritmo apresentado no artigo anterior. Continuo a achar que se trata de um algoritmo que traz mais vantagens na compreensão da divisão. É por esta razão que insisto novamente nesta técnica para dar resposta ao meu próprio repto - como utilizar esta técnica quando estão envolvidos números decimais.

Imagine-se então querer dividir dois números inteiros cujo quociente é um número decimal. Esta possibilidade nunca fica comprometida desde que o dividendo seja inferior ao divisor, por exemplo, a divisão entre 2 e 80.

(a)

Neste caso, para se poder continuar com a divisão é necessário aumentar um número suficiente de casas decimais ao dividendo até que se possa conseguir a divisão exacta. Assim, as duas unidades podem ser vistas como sendo 20 décimas, 200 centésimas ou 2000 milésimas… Neste exemplo, há a necessidade de considerar, pelo menos, 200 centésimas porque se trata do menor número onde posso formar, no mínimo, um grupo de 80.

Deste modo, há a necessidade de identificar a parte inteira e a decimal do quociente. Sugere-se então, o recurso a um traço vertical.

(b)

Agora procede-se normalmente ignorando a vírgula. Em 200 há duas vezes 80. Então, temos:

(c)

Havendo a necessidade de ainda dividir 40 centésimas, procura-se saber em 400 milésimas quantos grupos de 80 fazemos. Completa-se assim o algoritmo:

(d)

Portanto, 2:80=0,025

Outra situação que vale a pena referir, é quando surge uma divisão em que o dividendo tem menos casas decimais que o divisor, por exemplo, 452,5:1,25

(i)

Também aqui, a divisão deverá ser interpretada como sendo uma divisão por medição (subtracções sucessivas) onde se pretende saber, neste caso, em 45250 centésimas quantas 125 centésimas lá cabem. Posto isto, é nesta altura que se vai identificar, no quociente, a ordem das unidades. Esta ordem - as unidades, corresponde às centésimas do dividendo uma vez que se trata de dividir centésimas por centésimas.

(ii)

Agora, procede-se normalmente como se de uma divisão inteira se tratasse:

(iii)

Pode-se então escrever que 452,5:1,25=362

Se, eventualmente, a divisão não compreendesse um número inteiro de centésimas, o algoritmo continuaria a ser executado normalmente estando já identificado a parte decimal do quociente.

Por exemplo, o quociente entre 40,5 e 1,25 é um número inteiro de décimas. Fica o desafio para que o leitor, com este algoritmo, encontre esse valor.