Ultimamente tenho utilizado e praticado várias divisões com o algoritmo apresentado no artigo anterior. Continuo a achar que se trata de um algoritmo que traz mais vantagens na compreensão da divisão. É por esta razão que insisto novamente nesta técnica para dar resposta ao meu próprio repto - como utilizar esta técnica quando estão envolvidos números decimais.
Imagine-se então querer dividir dois números inteiros cujo quociente é um número decimal. Esta possibilidade nunca fica comprometida desde que o dividendo seja inferior ao divisor, por exemplo, a divisão entre 2 e 80.
(a)
Neste caso, para se poder continuar com a divisão é necessário aumentar um número suficiente de casas decimais ao dividendo até que se possa conseguir a divisão exacta. Assim, as duas unidades podem ser vistas como sendo 20 décimas, 200 centésimas ou 2000 milésimas… Neste exemplo, há a necessidade de considerar, pelo menos, 200 centésimas porque se trata do menor número onde posso formar, no mínimo, um grupo de 80.
Deste modo, há a necessidade de identificar a parte inteira e a decimal do quociente. Sugere-se então, o recurso a um traço vertical.
(b)
Agora procede-se normalmente ignorando a vírgula. Em 200 há duas vezes 80. Então, temos:
(c)
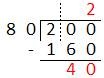
Havendo a necessidade de ainda dividir 40 centésimas, procura-se saber em 400 milésimas quantos grupos de 80 fazemos. Completa-se assim o algoritmo:
(d)
Portanto, 2:80=0,025
Outra situação que vale a pena referir, é quando surge uma divisão em que o dividendo tem menos casas decimais que o divisor, por exemplo, 452,5:1,25
(i)
Também aqui, a divisão deverá ser interpretada como sendo uma divisão por medição (subtracções sucessivas) onde se pretende saber, neste caso, em 45250 centésimas quantas 125 centésimas lá cabem. Posto isto, é nesta altura que se vai identificar, no quociente, a ordem das unidades. Esta ordem - as unidades, corresponde às centésimas do dividendo uma vez que se trata de dividir centésimas por centésimas.
(ii)
Agora, procede-se normalmente como se de uma divisão inteira se tratasse:
(iii)
Pode-se então escrever que 452,5:1,25=362
Se, eventualmente, a divisão não compreendesse um número inteiro de centésimas, o algoritmo continuaria a ser executado normalmente estando já identificado a parte decimal do quociente.
Por exemplo, o quociente entre 40,5 e 1,25 é um número inteiro de décimas. Fica o desafio para que o leitor, com este algoritmo, encontre esse valor.


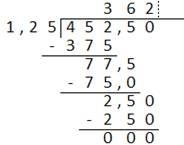
Sem comentários:
Enviar um comentário