A descoberta de relações numéricas pode ser vista como uma metodologia que, para além do desenvolvimento da capacidade de abstracção também favorece o raciocínio algébrico. É neste sentido que, numa visão matemática de natureza recreativa, proponho o desafio que poderá ser, também, uma ideia a aproveitar para ser levada à sala de aula na exploração de relações entre números pares e ímpares.
Considere-se então, os seguintes quadrados de papel com números inscritos em duas cores diferentes:
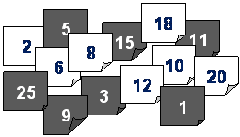 |
São necessárias duas caixas com as mesmas duas cores. O recurso ao origami poderá ser uma ajuda preciosa para a sua construção.
É pedido a uma pessoa que escolha dois papéis de cores diferentes e que os coloque, sem que ninguém veja, nas caixas. O objectivo é descobrir se os papéis colocados nas caixas respeitam, ou não, a correspondência das cores. Para isso é necessário recolher alguma informação matemática:
É necessário saber a soma do dobro do número que foi colocado na caixa branca com o triplo do número que foi colocado na caixa negra. Se a informação for verdadeira é o suficiente para saber se os papéis colocados nas caixas estão, ou não, com as cores trocadas.
Por exemplo, imagine-se que o valor da expressão é 46. Fico a saber que os papéis foram colocados com as cores trocadas nas caixas. Porquê?
Neste caso, o 5 (papel negro), foi colocado na caixa branca, o seu dobro é 10. O papel branco com o número 12 foi colado na caixa negra, cujo triplo é 36. A soma destes números é 46 (10+36).
De que forma poderá ser explicado este procedimento para ter a certeza que os papéis colocados nas caixas estão ou não de acordo com as suas cores?

1 comentário:
Seja B o número inscrito no papel colocado na caixa branca e N o número inscrito no papel colocado na caixa negra.
Sabemos que os números que constam nos papeis pretos são impares, enquanto os números que constam nos papeis brancos são pares.
Vamos averiguar se 2B+3N é par:
2B é sempre par.
A soma de um número par com qualquer outro número é um número par, se e só se esse número for, ele próprio, par.
Concluimos que se 2B+3N é par, então 3N é par. Ora se 3N é par, então N é par. Mas se N é par, então o papel é branco, pelo que não está colocada na caixa da sua cor.
Se 2B+3N é impar, então N é impar. Mas se N é impar, então o papel é negro, pelo que, concluimos, está colocado na caixa da sua cor.
Conclusão:
Se 2B+3N é par, os papeis não respeitam a correspondência das cores.
Se 2B+3N é impar, os papeis respeitam a correspondência das cores.
Enviar um comentário