Diga o que entende por média geométrica de um determinado conjunto de valores. Esta poderia ser uma questão de uma prova de avaliação de conhecimentos que, no âmbito dos conteúdos estudados naquele período, seria previsível que fosse posto à prova no próximo momento de avaliação. É por isso que no meu tempo de estudante, uma das estratégias adoptadas na preparação para as provas de avaliação, era decorar as definições que tínhamos no caderno diário. Neste caso, bastava decorar que a média geométrica de um determinado conjunto de dados é a raiz de índice n do produto desses valores elevados, cada um deles, à respectiva frequência absoluta.
A resposta correcta servia de garantia, para o professor, como o aluno se tinha apropriado daquele conceito. No entanto, o aluno continuava convicto de que aquele conhecimento não teria qualquer utilidade prática no futuro. A evolução do ensino da matemática acaba por valorizar a reflexão que o aluno faz sobre o seu próprio conhecimento ao ponto de retirar das provas de exames perguntas deste tipo. Se o aluno não consegue aplicar o conhecimento em novas situações, então é porque não se apropriou verdadeiramente do conceito matemático, logo, a avaliação feita não é a mais eficaz.
Imagine-se que em vez de ser pedida aquela definição, fosse pedido para determinar o comprimento do lado de um terreno com a forma de um quadrado que tivesse a mesma área de um outro terreno de 20m por 45m. Pretende-se, portanto, determinar a média geométrica destes dois valores. É o mesmo que encontrar um valor que, ao quadrado, seja igual ao produto de 20 por 45. O próprio aluno pode construir este conceito: área do terreno rectangular é 900m2 (20x45m2). Para se obter o lado de um quadrado com a mesma área basta determinar a raiz quadrada de 900. O procedimento efectuado traduz-se na seguinte expressão:
Não é mais que a aplicação da definição dada de média geométrica. Assim se chega à conclusão que 30 é a média geométrica de 20 e 45. A partir desta experiência matemática torna-se evidente a importância deste conceito matemático facilitando a sua compreensão e a automatização do algoritmo sem ter de recorrer à “gaveta” onde estava memorizada a definição. Também não se corre o risco da informação se perder no caso de a “gaveta” permanecer muito tempo fechada.
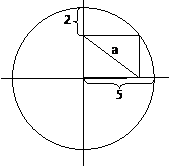
![clip_image005[5] clip_image005[5]](http://lh3.ggpht.com/_cutiQKPeNkA/SpF5eK1hvHI/AAAAAAAAAlc/6dgo_ZQVM4s/clip_image005%5B5%5D_thumb%5B4%5D.gif?imgmax=800) No caso do leitor querer avaliar o seu próprio conceito de média geométrica e a importância que lhe possa dar em outras situações do quotidiano, proponho o seguinte desafio: a partir da figura, crie uma situação problemática sem que utilize a expressão “média geométrica”, mas cuja resposta seja dada pela seguinte expressão:
No caso do leitor querer avaliar o seu próprio conceito de média geométrica e a importância que lhe possa dar em outras situações do quotidiano, proponho o seguinte desafio: a partir da figura, crie uma situação problemática sem que utilize a expressão “média geométrica”, mas cuja resposta seja dada pela seguinte expressão: