A pluralidade cultural é, sem dúvida, um dos aspectos mais positivos em resultado da migração humana. Há dias, quando visitava a Escola do 1º ciclo de Mação, a professora que dá apoio a uma criança chinesa procurou o meu parecer acerca da interpretação de um algoritmo feito por esta aluna. Tratava-se do algoritmo da divisão.
Será o algoritmo da divisão chinesa? O conhecimento que a criança tinha da língua portuguesa, já que eu não enxergo nada em chinês, não permitiu a comunicação de modo a chegar a essa conclusão. No entanto, sendo a matemática uma linguagem universal, fica-nos o registo desta criança que tentarei relatar.
Trata-se de uma técnica muito parecida com o nosso algoritmo tradicional da divisão, mas que, no meu entender, as suas diferenças potenciam uma melhor compreensão do processo de dividir.
Por exemplo, no caso de querer dividir 2586 por 8, o seu aspecto poderá ser o seguinte:
Ou ainda, no caso da aluna que tinha ainda a necessidade de registar as subtracções ao dividendo dos múltiplos de 8 que ia efectuando:
Pelo algoritmo, damos conta que o quociente é 323 e ainda restam 2, que ficam por dividir por 8 (divisor). Assim, simbolicamente poder-se-á escrever:
Na verdade, o procedimento é muito idêntico ao algoritmo indo-árabe a que estamos habituados. Apenas a disposição do divisor e do quociente mudam. Mas a opção de colocar o quociente por cima do dividendo permite interpretar, em qualquer momento do processo algorítmico, o valor de cada algarismo do quociente, uma vez que respeita sempre o seu valor de posição, tendo como referência o dividendo. Por outro lado, reduz a possibilidade de engano enquanto se fazem cálculos intermédios.
Trata-se de uma vantagem para aqueles mais desenvoltos no cálculo mental, permitindo adaptar o algoritmo às suas capacidades de forma a torná-lo mais rápido ou, eventualmente mais lento, se não tiver tão presente o domínio da tabuada.
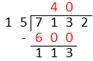
Vejamos o seguinte exemplo da divisão de 7132 por 15:
(a)
Para quem se sujeita, com frequência, a experiências de cálculo mental, não é difícil reconhecer imediatamente que 15x4=60 e por conseguinte, se a multiplicação fosse feita por 40, então obter-se-ia 600 em vez de 60. Neste caso, e porque se conseguiu aproximar de 713 dezenas, então dever-se-á ter o cuidado de colocar o número 40 na posição correspondente às dezenas. Basta respeitar o valor de posição, o zero do 40, por cima do algarismo três do 713.
(b)
Subtraindo as 600 dezenas, verifica-se que restam 113 que, afinal, ainda poderão ser divididos por 15. Se eventualmente insistir na ideia que o quádruplo de 15 é 60, então posso continuar com o algoritmo:
(c)
Verifica-se que ainda restam 53 dezenas. Teria agora a opção de proceder de forma idêntica. Ainda é possível formar nesta quantidade 3 grupos de 15. Mas, se juntar as duas unidades que faltam, e se o meu cálculo mental permitir reconhecer que 15x30=450, então poderei avançar desta forma:
(d)
Restam 82 unidades, portanto, ainda se pode formar 5 grupos de 15 (15x5=75). Assim, temos:
(e)
Finalmente, chega-se à conclusão que fazendo a divisão inteira de 7132 por 15 é possível formar 40 dezenas, mais 4 dezenas, mais 30 unidades e ainda mais 5 unidades de grupos de 15, e ainda restam 7 unidades.
Assim, sugere-se a finalização do algoritmo determinando a soma das partes do divisor:
(f)
Outra vantagem que vejo neste algoritmo, é no caso de se pretender determinar a divisão exacta, bastar acrescentar a vírgula ao dividendo e, para a direita dela, o número de ordens que se desejam envolver no cálculo. O mesmo já não acontece com o “nosso” algoritmo, dado que o registo do divisor limita esse procedimento o que poderá, nalguns casos, ter de se reiniciar a divisão com o cuidado de criar espaço para esse fim.
Havendo agora a necessidade de assimilar um pouco esta técnica para dividir, fica também lançado o repto aos leitores para a apresentação de sugestões de como dividir, com este algoritmo, números decimais.


![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg_UKHDZYS8X58HiFamtOKSaFGngafPDc34GSfsgtNjRzOjFhlzUEWA_peBm5LfAINn9DKIf11c3_9kUZV-EEoILgSMUri6CjgaXYI5CiH3XkDDFCW4pavhmn0IyvjMqpGFqExlBcrZ3xk/?imgmax=800)




1 comentário:
Interessante. Este algoritmo é muito parecido com o nosso, com a vantagem de que ele é um pouco mais organizado (pelo menos eu achei isso).
Enviar um comentário