Resto, excesso ou diferença

Quando mentalmente não se consegue efectuar a operação matemática desejada é nessa altura que se costuma recorrer ao algoritmo conhecido. Seguir um processo institucionalizado dá confiança a quem o pratica embora, por vezes, o praticante do algoritmo não atribua significado ao processo utilizado. Mas a aprendizagem matemática deve visar sempre a compreensão dos procedimentos e, por conseguinte, contribuir para se dar significado às rotinas.

Este objectivo não é um a meta fácil, principalmente nos primeiros anos de escolaridade onde é necessário o recurso a algoritmos para efectuar operações que ainda não foram conceptualizadas. A subtracção é o exemplo de uma operação que recorre a um algoritmo que, em caso pontuais, é de difícil compreensão. Refiro-me a situações em que é necessário recorrer a artifícios matemáticos para tornar possível esta operação, como seja nos casos de em que o algarismo do aditivo é inferior ao subtractivo.

A meu ver, a institucionalização do algoritmo só deve ocorrer quando o cálculo mental se revelar incapaz para se realizar a operação, ou quando outras técnicas utilizadas de forma compreensiva forem reconhecidas como sendo menos eficazes na obtenção de resultados mais rápidos. Mas o querer atingir objectivos muito rápidos no currículo do aluno faz com que a mecanização de procedimentos se antecipe à consolidação conceptual de respectiva operação.

No caso da subtracção, penso que seria importante analisar-se em primeiro lugar o significado da operação, pois pode tratar-se de um excesso, noutros casos de uma diferença ou ainda de um resto, dependendo do contexto onde se insere. Mas, à margem de situações concretas e abusando um pouco da abstracção matemática poder-se-á fazer uma breve análise a estes conceitos.

Por exemplo, 43 pode ser decomposto na adição 40 + 3 podendo, o 3, ser visto como sendo o resto que vai para além de 40. Portanto, perante a subtracção 43 – 40, poderemos entendê-la como querendo procurar o número que resta, para além do 40, para chegar ao 43.

Segundo este raciocínio e, tomando como outro exemplo a subtracção 54 – 26, pretendo determinar o que resta para além do 26 até ao 54. Assim, poderei decompor o 54 numa soma de duas parcelas de modo a obter 26. Este processo poderá ser feito de forma gradual de acordo com as capacidades de cálculo mental de cada utilizador, transferindo valores de uma parcela para a outra, criando adições equivalentes:

Uma outra interpretação seria por exemplo entender 54 – 26 como procurar a diferença que vai de 26 para 54. Neste caso, posso partir do 54 e ir retirando valor até atingir o 26. Depois basta adicionar os valores retirados;

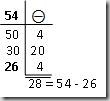
Por outro lado, 54 – 26 pode ser interpretado como sendo o excesso que vai além de 26 até 54. Neste caso poderia seguir outro procedimento que consta no apuramento do valor em excesso. A sua representação poderia ser a seguinte:

Estes são três exemplos de sugestões algorítmicas que podem ajudar a superar a dificuldade na subtracção quando o algarismo do aditivo é inferior ao subtractivo. Para além destas sugestões algorítmicas da subtracção, deixo a representação de uma outra que era muito usual antigamente. Por exemplo, a seguinte subtracção: 2546 - 1794.

Embora se trate de um algoritmo moroso, que vantagem lhe pode ser reconhecida em relação ao nosso algoritmo tradicional?